
The other formulas provided are usually more useful and represent the most common situations that physicists run into. An annulus of inner radius r 1 and moment of inertia for cirular cross section formula questions. This formula is the most "brute force" approach to calculating the moment of inertia. The moment of inertia formula for rectangle, circle, hollow and triangle beam sections have been given. Polar Moment Of Inertia - Definition, Formula, Uses. A new axis of rotation ends up with a different formula, even if the physical shape of the object remains the same. The method is demonstrated in the following examples. The consequence of this formula is that the same object gets a different moment of inertia value, depending on how it is rotating. Also, included are the formulas for the Parallel Axes Theorem (also known as Steiner Theorem), the rotation of axes, and the principal axes.
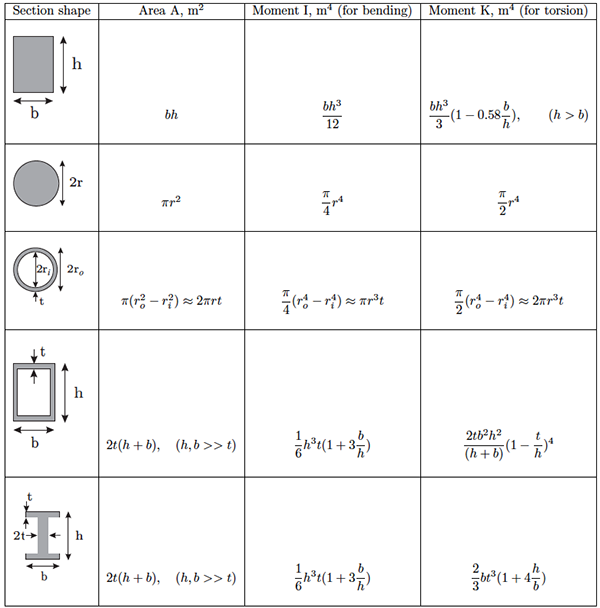
You do this for all of the particles that make up the rotating object and then add those values together, and that gives the moment of inertia. Basically, for any rotating object, the moment of inertia can be calculated by taking the distance of each particle from the axis of rotation ( r in the equation), squaring that value (that's the r 2 term), and multiplying it times the mass of that particle. For simple shapes such as squares, rectangles and circles, simple formulas have been worked out and the values must be calculated for each case. The general formula represents the most basic conceptual understanding of the moment of inertia. The general formula for deriving the moment of inertia. The formula for the moment of inertia uses distances from an axis, or, if you are using the fancier tensor formula, coordinates relative to an origin.


 0 kommentar(er)
0 kommentar(er)
